Skip to main content

Ambiguous Cylinder Illusion

How the ambiguous object works

In arts and entertainment, optical illusions have been used to create the impression of impossibility. In 2016, Professor Kokichi Sugihara in Japan found ambiguous cylinders that appear drastically different when viewed from two specific viewpoints. Suppose we have two viewers looking down on a curve floating above the \(xy-\)plane. The first viewer is a person looking at the curve, and the second viewer is in the mirror. We would like the two viewers to look down on the curve at 45-degree angles on opposite sides of the \(xy-\)plane. From the viewers’ perspectives, it looks as if they are viewing the curves and respectively, as shown in the following picture.
(https://m-repo.lib.meiji.ac.jp/dspace/bitstream/10291/19877/1/jma_12_1_2.pdf)

The key to the ambiguous cylinder is that the top of the cylinder is not a planar curve. This can be explained by the natural assumption of human visual perception. Natural assumption regard in visual depth three-dimensional object has width, height, and depth. As we know, two-dimensional figures don't have information on depth. But humans have the capacity to perceive a two-dimensional figure as a three-dimensional object. That's because our natural assumptions subconsciously add information on depth. When we see an illustration of an "impossible" object, we subconsciously try to perceive the object based on our natural assumptions.

Our design of an ambiguous cylinder

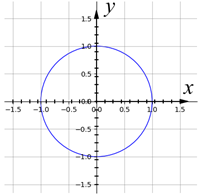
Our design consists of a curve of two diamonds and a curve of a circle. The curve of two diamonds is defined as following:
Upper part: \[y=\left\{\begin{split} \begin{aligned} &1+x, &-1 &\le x \lt -0.5 \\ &-x, &-0.5 &\le x \lt 0\\ &x, &0 &\le x \lt 0.5 \\ &1-x, &0.5 &\le x \le 1\\ \end{aligned} \end{split}\right.\] Lower part: \[y=\left\{\begin{split} \begin{aligned} &-1-x, &-1 &\le x \lt -0.5 \\ &x, &-0.5 &\le x \lt 0\\ &-x, &0 &\le x \lt 0.5 \\ &-1+x, &0.5 &\le x \le 1\\ \end{aligned} \end{split}\right.\]
The curve of a unit circle is defined as following: \[x^2+y^2=1\]
We design a cylinder with OpenSCAD to show these two different curves. From the viewers’ perspectives, it looks as if they are viewing two curves respectively. The design looks like a vertical cylinder, but its section appears to be different; in one view it appears to be two diamonds, while in the other view it appears to a circle.

Why to use this design

  1. The two curves in this design are different enough to show the ambiguous cylinder illusion. Our design looks like a circular cylinder from the front and a two-diamond cylinder in the mirror. It is a magic phenomenon. The direct views of the objects and their mirror images generate quite different interpretations of the 3D shapes. We cannot correct our interpretations although we logically know that they come from the same objects. Even if the object is rotated in front of a viewer, it is difficult to understand the true shape of the object, and thus the illusion does not disappear.
  2. The unusual visual effects of ambiguous cylinder illusion might be useful. At least upon one's first encounter with ambiguous cylinders, they are surprising and mysterious. Optical illusions including ambiguous cylinders are potential resources for new products in many fields such as education, architecture, art, entertainment, advertising, and tourism. In the above design, we investigate the magic phenomenon of ambiguous cylinder illusion. This helps us to better understand the process of human visual perception.
In the above design, we investigate the magic phenomenon of ambiguous cylinder illusion. This helps us to better understand the process of human visual perception.

Comments

Post a Comment

Popular posts from this blog

The Approximation of a Solid of Revolution

Most math teachers I've had have been able to break down Calculus into two very broad categories: derivatives and integrals. What is truly amazing, is how much you can do with these two tools. By using integration, it is possible to approximate the shape of a 2-D function that is rotated around an axis. This solid created from the rotation is known as a solid of revolution. To explain this concept, we will take a look at the region bounded by the two functions: \[ f(x) = 2^{.25x} - 1 \] and \[ g(x) = e^{.25x} - 1 \] bounded at the line y = 1. This region is meant to represent a cross section of a small bowl. While it may not perfectly represent this practical object, the approximation will be quite textured, and will provide insight into how the process works. The region bounded by the two functions can be rotated around the y-axis to create a fully solid object. This is easy enough to talk about, but what exactly does this new solid look like? Is...
8 comments
Read more

Solids of Revolution Revisited

Introduction In my previous blog post on solids of revolution, we looked at the object formed by rotating the area between \(f(x) = -\frac{1}{9}x^2+\frac{3}{4} \) and \( g(x)=\frac{1}{2}-\frac{1}{2}e^{-x} \) around the \( x \) axis and bounded by \( x = 0 \) and \( x = 1.5 \). When this solid is approximated using 10 washers, the resulting object looks like this: When I was looking back over the 3D prints I’d created for this course, I noticed that the print for this example was the least interesting of the bunch. Looking at the print now, I feel like the shape is rather uninteresting. The curve I chose has such a gradual slope that each of the washers are fairly similar in size and causes the overall shape to just look like a cylinder. Since calculating the changes in the radiuses of the washers is a big part of the washer method, I don’t think this slowly decreasing curve was the best choice to illustrate the concept. The reason I had done this o...
Post a Comment
Read more

Finding the Center of Mass of a Toy Boat

Consider two people who visit the gym a substantial amount. One is a girl who loves to lift weights and bench press as much as she possibly can. The other is a guy who focuses much more on his legs, trying to break the world record for squat weight. It just so happens that these two are the same height and have the exact same weight, but the center of their weight is not in the same part of their body. This is because the girl has much more weight in the top half of her body and the boy has more weight in the bottom half. This difference in center of mass is a direct result of the different distributions of mass throughout both of their bodies. Moments and Mass There are two main components to finding the center of mass of an object. The first, unsurprisingly, is the mass of the whole object. In this case of the boat example, the mass will be uniform throughout the entire object. This is ideal a majority of the time as it drastically reduces the difficulty...
Post a Comment
Read more