Skip to main content

    In mathematics, the calculation of volume is an indispensable part. However, in real-life construction and various productions, the volume we require to calculate cannot be simply calculated like: long * width * high. So for all kinds of odd-shaped parts, if we want to know its volume (for example, how much material is needed to make a certain item), one of the ways is to divide it into many small cross-sections and perform step-by-step calculations ( You can also put it directly into a container filled with water, and then look at the volume of water discharged, I think this method is simpler, but not everything can be put in the water, is’t it?).

    To give a very simple example, to calculate the volume of a dumpling, direct calculation may not be very simple, but we can divide it into many parts longitudinally, so that each part looks like a triangle. By calculating the volume of each part, Then add up to get a relatively accurate value. The more data points, the closer to the real volume.
    I used two simpler equations: y=0.5\sin x and y=-0.5\sin x, They can intersect a lot of "dumplings"
    The intersection of the two functions is at (kπ, 0), k ∈ 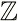整数集. So We take out one of the "dumplings":
    Then its overall length is from (0, 0) to (π, 0), we divide it into 15 parts to calculate, assuming that the cross section of each part is a regular triangle. The height of each serving is 0.20943.


    Modeling through these data, we can get this

    We add up all the volumes and we can get that the volume of "dumplings" is about 1.36026.
    
    So, next calculate the real volume of this "dumpling", we use the function 
∫ (0.5sinx-(-0.5sinx))*(sinπ/3)*(0.5sinx-(-0.5sinx))dx from 0 to π to calculate, The function in the middle can be simplified to sinx*sinx*(sinπ/3). After calculation, the final score is 1.36034. The two scores are very close. This is a very simple and easy to show example. Relatively speaking, it is also a special but very common Chinese food, so I hope it will help to understand this method.
    
Labels:

Comments

Post a Comment

Popular posts from this blog

Knot 9-31

Knot 9-31 A knot is mathematics is defined as a closed, non-self-intersecting curve that is placed in three dimensions and cannot be the "unknot". The main difference between a knot in the real world and a known in mathematics is that a knot in mathematics does not contain any extra strands. The example following will help visualize this. Today, I have specifically chosen knot 9-31 from the Knot Atlas. This knot is very unique and contains some very interesting properties that we are going to look into. The Crossing Number For my knot today, I chose knot 9-31 from the Knot Atlas. This knot contains 9 crossings! The Unknotting Number The unknotting number is exactly what is sounds like. This is the minimum number of times the knot must be passed through itself to untie it. Luckily, the Knot Atlas is super useful and provides the unknotting number for us, but I still...
Post a Comment
Read more

Do Over: Integration for Over Regions in the Plane

Introduction Earlier in the semester, we visited the topic of integration for over region regions in the plane. This was our first experience with taking integration in the third dimension. To do this, we had to use double integrals to calculate the volume of a region between two surfaces. This topic seems relatively straightforward and anyone who has taken a higher calculus class knows of double integrals. Today, we are going to revisit this topic for a couple of reasons. Why Double Integrals Again? As mentioned before, I am revisiting this topic for a couple of reasons. One of the main reasons is due to how the 3D print turned out. Due to the function, I chose, the final rectangular prism was stand alone. When printing, this resulted in a sloppy prism that lacked structural integrity. The image below is a reference to my original design that includes the prism that had the issue. The main cause of ...
Post a Comment
Read more

Middle of Mass Measured from Moment

The center of mass of an object is the point that lies in the average position of mass in that object. For a normal polygon, that point is in the middle of the shape. However, if the shape is irregular, has concave angles, or has holes, the center of mass can be far from the middle of the object. Two things come into factor when determining the center of mass of an object. Weight and distance. Obviously, if one side of an object has more mass than the other, the center of mass will be on the heavier side. But, distance plays a role, too. If two sides of an object have the same mass, but one is farther from the middle, the center of mass will be on the side that has farther mass. Multiplying both of these factors together gives the moment of an object. Dividing the moment by the overall mass gives the location of the center of mass.   The reason I chose my shape is to mimic how those toy balancing birds work. The toy is a model bird with its wings outstretched. The ...
Post a Comment
Read more